Basic QC Practices
Break all the rules, part 3 - answers
The answers to the most complex control situation - how to interpret "Westgard Rules" when there are 3 controls at different levels.
Break All the Rules, Part Three: The Answers!
Sten Westgard, MS
August 2017
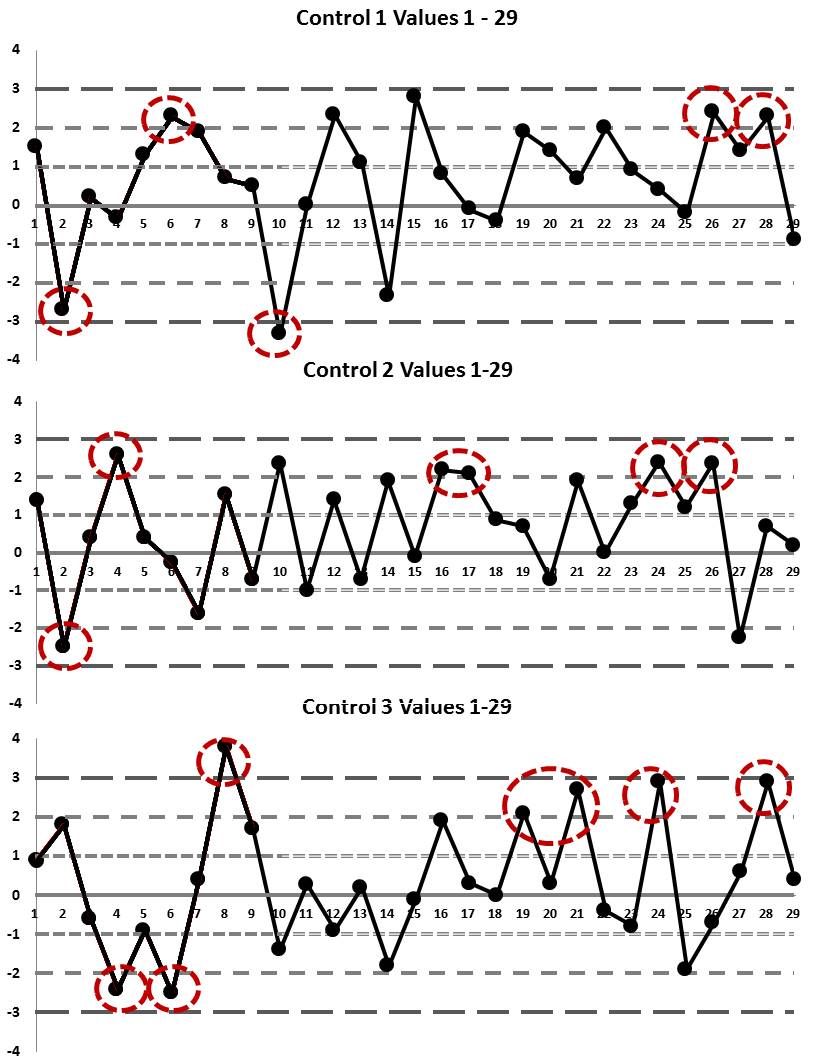
Here we finally reveal the interpretation of using 3 levels of "Westgard Rules". It's the trickiest set of control data yet, looking at the 1:3s/2of3:2s/R:4s/3:1s/6:x across all levels and all runs. After run 77, apply the 9:x rule. After run 103, apply the 12:x rule.
The tables and graphs
The following data set is going to have a low control with a mean of 47 and an SD of 3 and a middle control with a mean of 71 and an SD of 8 and a high control of 256 with an SD of 18. I'm not going to tell you which test or what units are involved. They're irrelevant to this exercise. We're also not going to look at the total allowable error or CV or bias. All of that becomes important after we know the basics of QC and charting.
To make it a little easier to understand this data, here are the Levey-Jennings charts for these first 29 values (notice for each control, not only is the raw value given, but the z-score is shown as well - that's really useful):
Runs 1 through 29:
|
Values |
Control 1 |
1 z |
Control 2 |
2-z |
Control 3 |
3 -z |
RULE |
|
Run 1 |
51.5 |
1.5 |
82.2 |
1.4 |
272.2 |
0.9 |
|
|
Run 2 |
38.9 |
-2.7 |
51 |
-2.5 |
288.4 |
1.8 |
2of3:2s |
|
Run 3 |
47.6 |
0.2 |
74.2 |
0.4 |
245.2 |
-0.6 |
|
|
Run 4 |
46 |
-0.33333 |
91.8 |
2.6 |
212.8 |
-2.4 |
R:4s |
|
Run 5 |
50.9 |
1.3 |
74.2 |
0.4 |
239.8 |
-0.9 |
|
|
Run 6 |
53.9 |
2.3 |
69 |
-0.25 |
211 |
-2.5 |
R:4s |
|
Run 7 |
52.7 |
1.9 |
58.2 |
-1.6 |
263.2 |
0.4 |
|
|
Run 8 |
49.1 |
0.7 |
83.3 |
1.54 |
324.4 |
3.8 |
1:3s |
|
Run 9 |
48.5 |
0.5 |
65.4 |
-0.7 |
286.6 |
1.7 |
|
|
Run 10 |
37 |
-3.33 |
90 |
2.375 |
230.8 |
-1.4 |
1:3s |
|
Run 11 |
47 |
0 |
63 |
-1 |
261.0 |
0.28 |
|
|
Run 12 |
54 |
2.333333 |
82.2 |
1.4 |
239.8 |
-0.9 |
|
|
Run 13 |
50.3 |
1.1 |
65.4 |
-0.7 |
259.6 |
0.2 |
|
|
Run 14 |
40 |
-2.33333 |
86.2 |
1.9 |
223.6 |
-1.8 |
|
|
Run 15 |
55.4 |
2.8 |
70.2 |
-0.1 |
254.2 |
-0.1 |
2of3:2s |
|
Run 16 |
49.4 |
0.8 |
88.6 |
2.2 |
290.2 |
1.9 |
|
|
Run 17 |
46.7 |
-0.1 |
87.8 |
2.1 |
261.4 |
0.3 |
|
|
Run 18 |
45.8 |
-0.4 |
78 |
0.875 |
256 |
0.0 |
|
|
Run 19 |
52.7 |
1.9 |
76.6 |
0.7 |
293.8 |
2.1 |
2of3:2s |
|
Run 20 |
51.2 |
1.4 |
65.4 |
-0.7 |
261.4 |
0.3 |
|
|
Run 21 |
49 |
0.667 |
86.2 |
1.9 |
304.6 |
2.7 |
|
|
Run 22 |
53 |
2 |
71 |
0 |
248.8 |
-0.4 |
|
|
Run 23 |
49.7 |
0.9 |
81.4 |
1.3 |
241.6 |
-0.8 |
|
|
Run 24 |
48.2 |
0.4 |
90.2 |
2.4 |
308.2 |
2.9 |
2of3:2s |
|
Run 25 |
46.4 |
-0.2 |
80.6 |
1.2 |
221.8 |
-1.9 |
|
|
Run 26 |
54.2 |
2.4 |
90 |
2.375 |
243.4 |
-0.7 |
2of3:2s |
|
Run 27 |
51.2 |
1.4 |
53 |
-2.25 |
266.8 |
0.6 |
|
|
Run 28 |
53.9 |
2.3 |
76.6 |
0.7 |
308.2 |
2.9 |
2of3:2s |
|
Run 29 |
44.3 |
-0.9 |
72.6 |
0.2 |
263.2 |
0.4 |
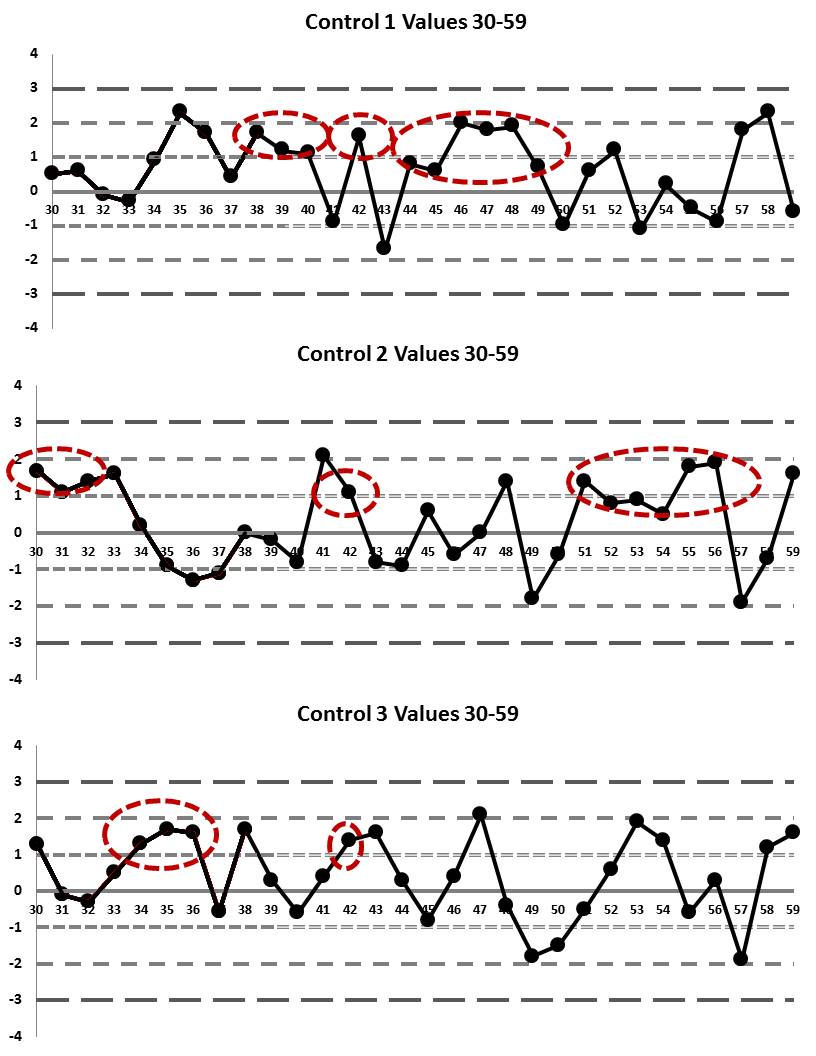
Runs 30 through 59:
|
Values |
Control 1 |
1 z |
Control 2 |
2 z |
Control 3 |
3 z |
Rule |
|
30 |
48.5 |
0.5 |
84.6 |
1.7 |
279.4 |
1.3 |
3:1s |
|
31 |
48.8 |
0.6 |
79.8 |
1.1 |
254.2 |
-0.1 |
|
|
32 |
46.7 |
-0.1 |
82.2 |
1.4 |
250.6 |
-0.3 |
|
|
33 |
46.1 |
-0.3 |
83.8 |
1.6 |
265 |
0.5 |
|
|
34 |
49.7 |
0.9 |
72.6 |
0.2 |
279.4 |
1.3 |
3:1s |
|
35 |
53.9 |
2.3 |
63.8 |
-0.9 |
286.6 |
1.7 |
|
|
36 |
52.1 |
1.7 |
60.6 |
-1.3 |
284.8 |
1.6 |
|
|
37 |
48.2 |
0.4 |
62.2 |
-1.1 |
245.8 |
-0.6 |
|
|
38 |
52.1 |
1.7 |
71 |
0 |
286.6 |
1.7 |
3:1s |
|
39 |
50.6 |
1.2 |
69.4 |
-0.2 |
261.4 |
0.3 |
|
|
40 |
50.3 |
1.1 |
64.6 |
-0.8 |
245.2 |
-0.6 |
|
|
41 |
44.3 |
-0.9 |
87.8 |
2.1 |
263.2 |
0.4 |
|
|
42 |
51.8 |
1.6 |
79.8 |
1.1 |
281.2 |
1.4 |
3:1s |
|
43 |
41.9 |
-1.7 |
64.6 |
-0.8 |
284.8 |
1.6 |
|
|
44 |
49.4 |
0.8 |
63.8 |
-0.9 |
261.4 |
0.3 |
6:x |
|
45 |
48.8 |
0.6 |
75.8 |
0.6 |
241.6 |
-0.8 |
|
|
46 |
49.9 |
0.97 |
66.2 |
-0.6 |
263.2 |
0.4 |
|
|
47 |
52.4 |
1.8 |
71 |
0 |
293.8 |
2.1 |
|
|
48 |
52.7 |
1.9 |
82.2 |
1.4 |
248.8 |
-0.4 |
|
|
49 |
49.1 |
0.7 |
56.6 |
-1.8 |
223.6 |
-1.8 |
|
|
50 |
44 |
-1 |
66.2 |
-0.6 |
229 |
-1.5 |
|
|
51 |
48.8 |
0.6 |
82.2 |
1.4 |
247 |
-0.5 |
6:x |
|
52 |
50.6 |
1.2 |
77.4 |
0.8 |
266.8 |
0.6 |
|
|
53 |
43.7 |
-1.1 |
78.2 |
0.9 |
290.2 |
1.9 |
|
|
54 |
47.6 |
0.2 |
75 |
0.5 |
281.2 |
1.4 |
|
|
55 |
45.5 |
-0.5 |
85.4 |
1.8 |
245.2 |
-0.6 |
|
|
56 |
44.3 |
-0.9 |
86.2 |
1.9 |
261.4 |
0.3 |
|
|
57 |
52.4 |
1.8 |
55.8 |
-1.9 |
221.8 |
-1.9 |
|
|
58 |
53.9 |
2.3 |
65.4 |
-0.7 |
277.6 |
1.2 |
|
|
59 |
45.2 |
-0.6 |
83.8 |
1.6 |
284.8 |
1.6 |
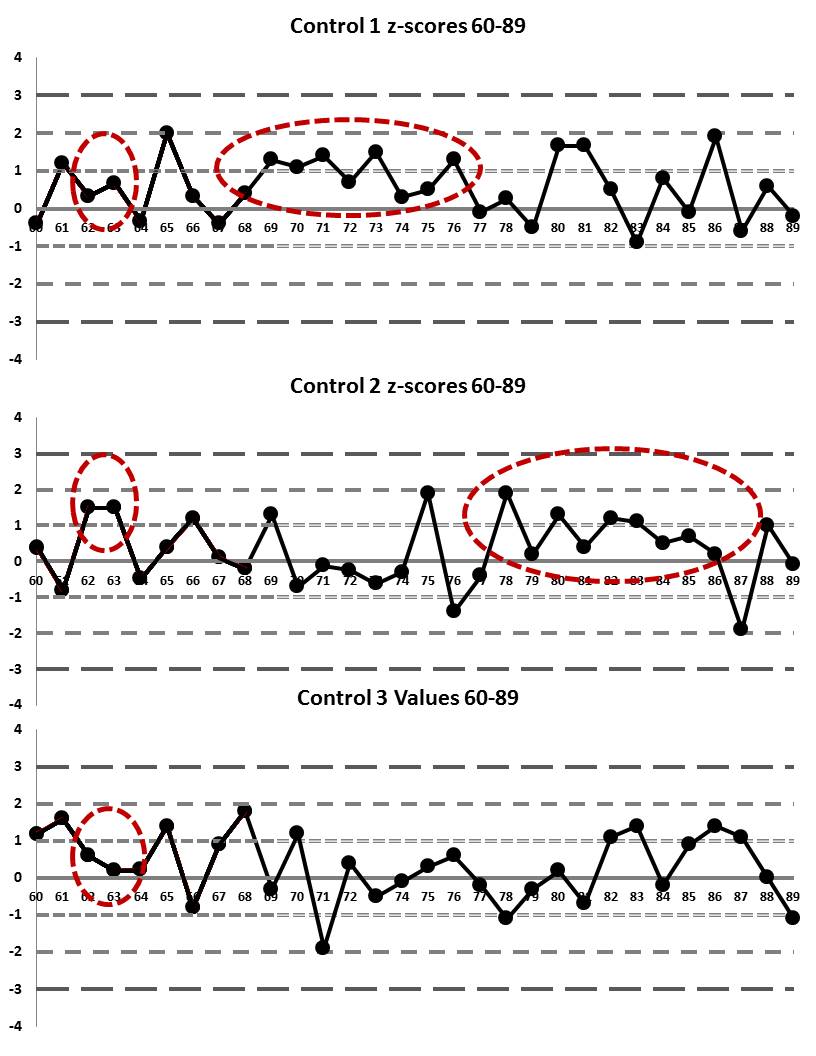
Runs 60 through 89:
|
Values |
Control 1 |
z 1 |
Control 2 |
Z 2 |
Control 3 |
z 3 |
Rule |
|
60 |
45.8 |
-0.4 |
74.2 |
0.4 |
277.6 |
1.2 |
|
|
61 |
50.6 |
1.2 |
64.6 |
-0.8 |
284.8 |
1.6 |
|
|
62 |
48 |
0.3 |
83 |
1.5 |
266.8 |
0.6 |
6:x |
|
63 |
49 |
0.7 |
83 |
1.5 |
259.6 |
0.2 |
|
|
64 |
46 |
-0.3 |
67.1 |
-0.49 |
260.1 |
0.23 |
|
|
65 |
53 |
2.0 |
74.2 |
0.4 |
281.2 |
1.4 |
|
|
66 |
48 |
0.3 |
80.6 |
1.2 |
241.6 |
-0.8 |
|
|
67 |
45.8 |
-0.4 |
71.8 |
0.1 |
272.2 |
0.9 |
|
|
68 |
48.2 |
0.4 |
69.4 |
-0.2 |
288.4 |
1.8 |
9:x |
|
69 |
50.9 |
1.3 |
81.4 |
1.3 |
250.6 |
-0.3 |
|
|
70 |
50.3 |
1.1 |
65.4 |
-0.7 |
277.6 |
1.2 |
|
|
71 |
51.2 |
1.4 |
70 |
-0.125 |
221.8 |
-1.9 |
|
|
72 |
49.1 |
0.7 |
69 |
-0.25 |
263.2 |
0.4 |
|
|
73 |
51.5 |
1.5 |
66 |
-0.625 |
247 |
-0.5 |
|
|
74 |
47.9 |
0.3 |
68.6 |
-0.3 |
254.2 |
-0.1 |
|
|
75 |
48.5 |
0.5 |
86.2 |
1.9 |
261.4 |
0.3 |
|
|
76 |
50.9 |
1.3 |
59.8 |
-1.4 |
266.8 |
0.6 |
|
|
77 |
46.7 |
-0.1 |
67.8 |
-0.4 |
252.4 |
-0.2 |
|
|
78 |
47.8 |
0.3 |
86.2 |
1.9 |
236.2 |
-1.1 |
9:x |
|
79 |
45.5 |
-0.5 |
72.6 |
0.2 |
250.6 |
-0.3 |
|
|
80 |
52 |
1.7 |
81.4 |
1.3 |
259.6 |
0.2 |
|
|
81 |
52 |
1.7 |
74.2 |
0.4 |
243.4 |
-0.7 |
|
|
82 |
48.5 |
0.5 |
80.6 |
1.2 |
275.8 |
1.1 |
|
|
83 |
44.3 |
-0.9 |
79.8 |
1.1 |
281.2 |
1.4 |
|
|
84 |
49.4 |
0.8 |
75 |
0.5 |
252.4 |
-0.2 |
|
|
85 |
46.7 |
-0.1 |
76.6 |
0.7 |
272.2 |
0.9 |
|
|
86 |
52.7 |
1.9 |
72.6 |
0.2 |
281.2 |
1.4 |
|
|
87 |
45.2 |
-0.6 |
55.8 |
-1.9 |
275.8 |
1.1 |
|
|
88 |
48.8 |
0.6 |
79 |
1 |
256 |
0 |
|
|
89 |
46.4 |
-0.2 |
70.2 |
-0.1 |
236.2 |
-1.1 |
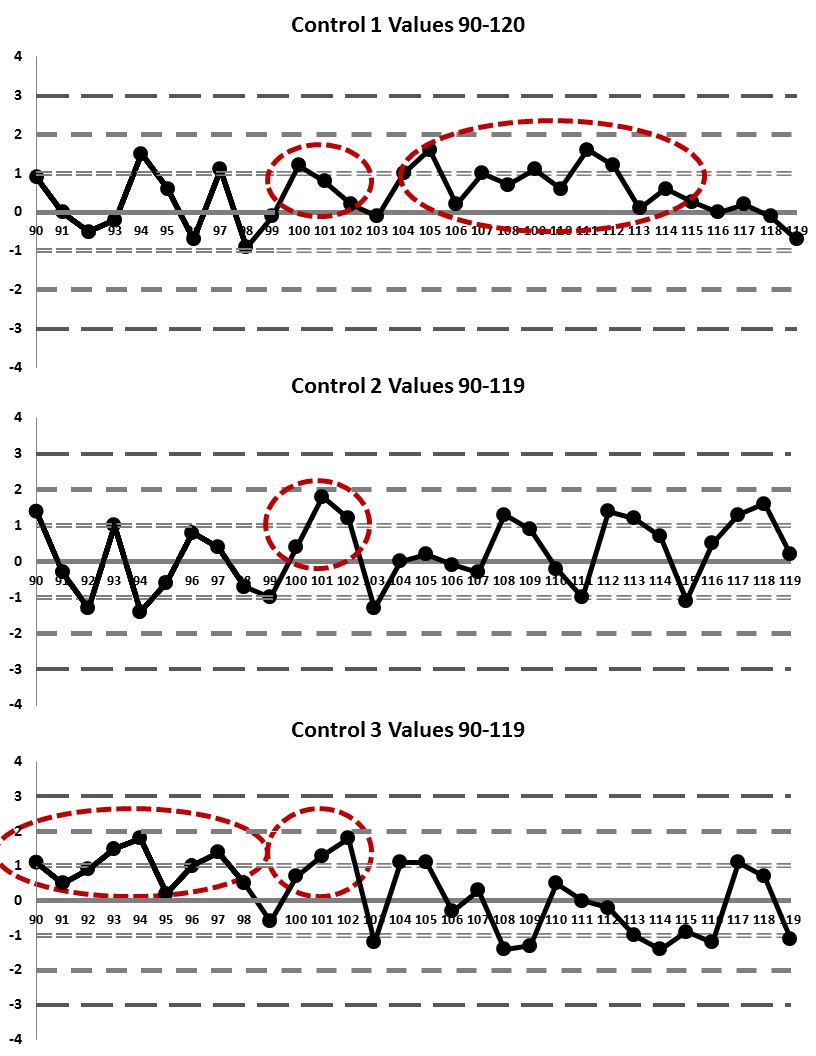
Runs 90 through 119:
|
Values |
Control 1 |
Z 1 |
Control 2 |
Z 2 |
Control 3 |
Z 3 |
Rules |
|
90 |
49.7 |
0.9 |
82.2 |
1.4 |
275.8 |
1.1 |
9:x |
|
91 |
47 |
0 |
68.6 |
-0.3 |
265 |
0.5 |
|
|
92 |
45.5 |
-0.5 |
60.6 |
-1.3 |
272.2 |
0.9 |
|
|
93 |
46.4 |
-0.2 |
79 |
1 |
283 |
1.5 |
|
|
94 |
51.5 |
1.5 |
59.8 |
-1.4 |
288.4 |
1.8 |
|
|
95 |
48.8 |
0.6 |
66.2 |
-0.6 |
259.6 |
0.2 |
|
|
96 |
44.9 |
-0.7 |
77.4 |
0.8 |
274 |
1 |
|
|
97 |
50.3 |
1.1 |
74.2 |
0.4 |
281.2 |
1.4 |
|
|
98 |
44.3 |
-0.9 |
65.4 |
-0.7 |
265 |
0.5 |
|
|
99 |
46.7 |
-0.1 |
63 |
-1 |
245.2 |
-0.6 |
|
|
100 |
50.6 |
1.2 |
74.2 |
0.4 |
268.6 |
0.7 |
9:x |
|
101 |
49.4 |
0.8 |
85.4 |
1.8 |
279.4 |
1.3 |
|
|
102 |
47.6 |
0.2 |
80.6 |
1.2 |
288.4 |
1.8 |
|
|
103 |
46.7 |
-0.1 |
60.6 |
-1.3 |
234.4 |
-1.2 |
|
|
104 |
50 |
1 |
71 |
0 |
275.8 |
1.1 |
12:x |
|
105 |
51.8 |
1.6 |
72.6 |
0.2 |
275.8 |
1.1 |
|
|
106 |
47.6 |
0.2 |
70.2 |
-0.1 |
250.6 |
-0.3 |
|
|
107 |
50 |
1 |
68.6 |
-0.3 |
261.4 |
0.3 |
|
|
108 |
49.1 |
0.7 |
81.4 |
1.3 |
230.8 |
-1.4 |
|
|
109 |
50.3 |
1.1 |
78.2 |
0.9 |
232.6 |
-1.3 |
|
|
110 |
48.8 |
0.6 |
69.4 |
-0.2 |
265 |
0.5 |
|
|
111 |
51.8 |
1.6 |
63 |
-1 |
256 |
0 |
|
|
112 |
50.6 |
1.2 |
82.2 |
1.4 |
252.4 |
-0.2 |
|
|
113 |
47.3 |
0.1 |
80.6 |
1.2 |
238 |
-1 |
|
|
114 |
48.8 |
0.6 |
76.6 |
0.7 |
230.8 |
-1.4 |
|
|
115 |
47.8 |
0.3 |
62.2 |
-1.1 |
239.8 |
-0.9 |
|
|
116 |
47 |
0 |
75 |
0.5 |
234.4 |
-1.2 |
|
|
117 |
47.6 |
0.2 |
81.4 |
1.3 |
275.8 |
1.1 |
|
|
118 |
46.7 |
-0.1 |
83.8 |
1.6 |
268.6 |
0.7 |
|
|
119 |
44.9 |
-0.7 |
72.6 |
0.2 |
236.2 |
-1.1 |
Runs 120 through 150:
|
Values |
Control 1 |
Z 1 |
Control 2 |
Z 2 |
Control 3 |
Z 3 |
Rules |
|
120 |
46.7 |
-0.1 |
62.2 |
-1.1 |
239.8 |
-0.9 |
|
|
121 |
47 |
0 |
75 |
0.5 |
234.4 |
-1.2 |
12:x |
|
122 |
47.6 |
0.2 |
81.4 |
1.3 |
275.8 |
1.1 |
|
|
123 |
46.7 |
-0.1 |
83.8 |
1.6 |
268.6 |
0.7 |
|
|
124 |
44.9 |
-0.7 |
72.6 |
0.2 |
236.2 |
-1.1 |
|
|
125 |
50.9 |
1.3 |
79 |
1 |
263.2 |
0.4 |
|
|
126 |
52.7 |
1.9 |
76.6 |
0.7 |
230.8 |
-1.4 |
|
|
127 |
46.4 |
-0.2 |
80.6 |
1.2 |
232.6 |
-1.3 |
|
|
128 |
44 |
-1 |
75.8 |
0.6 |
270.4 |
0.8 |
|
|
129 |
51.2 |
1.4 |
86.2 |
1.9 |
268.6 |
0.7 |
|
|
130 |
48.5 |
0.5 |
80.6 |
1.2 |
252.4 |
-0.2 |
|
|
131 |
49.1 |
0.7 |
75.8 |
0.6 |
238 |
-1 |
|
|
132 |
51.8 |
1.6 |
75.8 |
0.6 |
248.8 |
-0.4 |
|
|
133 |
42.2 |
-1.6 |
58.2 |
-1.6 |
254.2 |
-0.1 |
|
|
134 |
43.4 |
-1.2 |
70.2 |
-0.1 |
265 |
0.5 |
12:x |
|
135 |
50.3 |
1.1 |
69.4 |
-0.2 |
279.4 |
1.3 |
|
|
136 |
49.1 |
0.7 |
72.6 |
0.2 |
284.8 |
1.6 |
|
|
137 |
43.7 |
-1.1 |
70.2 |
-0.1 |
259.6 |
0.2 |
|
|
138 |
48.2 |
0.4 |
65.4 |
-0.7 |
274 |
1 |
|
|
139 |
42.8 |
-1.4 |
81.4 |
1.3 |
268.6 |
0.7 |
|
|
140 |
43.1 |
-1.3 |
78.2 |
0.9 |
277.6 |
1.2 |
|
|
141 |
48.8 |
0.6 |
69.4 |
-0.2 |
266.8 |
0.6 |
|
|
142 |
49.1 |
0.7 |
63 |
-1 |
290.2 |
1.9 |
|
|
143 |
46.4 |
-0.2 |
82.2 |
1.4 |
277.6 |
1.2 |
|
|
144 |
44 |
-1 |
75 |
0.5 |
266.8 |
0.6 |
|
|
145 |
45.8 |
-0.4 |
76.6 |
0.7 |
266.8 |
0.6 |
|
|
146 |
45.5 |
-0.5 |
59 |
-1.5 |
243.4 |
-0.7 |
|
|
147 |
51.2 |
1.4 |
81.4 |
1.3 |
266.8 |
0.6 |
|
|
148 |
48.5 |
0.5 |
78.2 |
0.9 |
277.6 |
1.2 |
12:x |
|
149 |
49.1 |
0.7 |
73.4 |
0.3 |
266.8 |
0.6 |
|
|
150 |
50.3 |
1.1 |
75 |
0.5 |
270.4 |
0.8 |
Summary of Rules Violated
- 1:3s is violated 2 times
- 2of3:2s is violated 6 times
- R:4s is violated 2 times
- 3:1s is violated 4 times
- 6:x is violated 3 times
- 9:x is violated 4 times
- 12:x is violated 4 times
If there were any differences between your interpretations and ours, they were probably for the following reasons
- We were looking ACROSS-levels as well as WITHIN-levels, as well as ACROSS-runs. If you missed that step, you miss out on a lot of errors
- We are applying the rules in the order, as specified with the designated "Westgard Rules" sequence: 1:3s/2of3:2s/R:4s/3:1s/6:x. with 9:x and 12:x being used later. If a 2of3:2s violation occurs, then a 3:1s violation in the same data set doesn't matter, nor would a 6:x, etc.
- We interpreted control violations in numerical order, starting with run 1, then proceeding sequentially. If you just look at the charts and just look for the most visually outstanding errors, you may miss an error. Also, if an error is found in a previous run, then that data isn't allowed to be used in other rule interpretations. So an error found earlier in the sequence will mean that all data from that point and earlier cannot be used in the interpretations.
- there are probably more rule violations in this example than a lab would see in a whole year (I hope), so having these errors occur so quickly one after another is undoubtedly a strange situation