Basic Method Validation

No, this doesn't involve making clones (we'll leave that to the Scots). This article is about one of the gold standards in method comparison studies. Dr. Westgard explains what this important experiment is, how you perform and interpret it, as well as how you can use the results to improve your laboratory. A Javascript Replication Experiment calculator is included to crunch the numbers for you

MV - The Replication Experiment

• Purpose
• Factors to consider
  • Time period of experiment
  • Matrix of sample
  • Number of materials and concentrations to be tested
  • Number of test samples
• Data Calculations
• A Javascript calculator
• Criteria for acceptable performance
• Recommended minimum studies
• References

Purpose

A replication experiment is performed to estimate the imprecision or random error of the analytical method. Methods of measurements are almost always subject to some random variation. Recall our bathroom scale illustration of random and systematic errors in MV - The Experimental Plan, as well as the graphical descriptions in MV - The inner, hidden, deeper, secret meaning. Repeat measurements will usually reveal slightly different results, sometimes a little higher, sometimes a little lower. Determining the amount of random error is usually one of the first steps in a method validation study.

A replication experiment is typically performed by obtaining test results on 20 samples of the same material and then calculating the mean, standard deviation, and coefficient of variation. The purpose is to observe the variation expected in a test result under the normal operating conditions of the laboratory. Ideally, the test variation should be small, i.e., all the answers on the repeated measurements should be nearly the same.

The replication experiment estimates the random error caused by factors that vary in the operation of the method, such as the pippetting of samples, the reaction conditions that depend on timing, mixing, temperature, and heating, and even the measurement itself. In non-automated systems, variation in the techniques of individual analysts may be a large contributor to the observed variation of a test. With automated systems, the lack of uniformity and the instability of instrument and reaction conditions may still cause small variations that may again show up as positive and negative variations in the final test results. While the exact effect can't be predicted at any moment, the distribution of these effects over time can be predicted to provide estimates of how large the random error might be.

Factors to consider

The amount of random error that will be observed depends on the experimental design because certain variables may not show up unless the right conditions are chosen. For example, when an experiment is performed in a short period of time, say within an analytical run, the effects of long term variation due to day-to-day changes in operating conditions will not be observed. Room temperature may be constant in that short time period, whereas it might vary more over a day, on different days, and in different seasons. Important factors for designing the experiment are the time period of the experiment, the matrix of the samples to be tested, the number and concentration of materials to be tested, and the number of samples to be analyzed. While it is expected that the number of analysts who perform the test may also be a factor, this variable is generally controlled during method validation studies and only one or a few well-trained analysts are involved in these studies.

Time period of experiment

The length of time over which the experiment is conducted is critical for the interpretation of the data and the conclusion that may be drawn. When samples are analyzed within a single analytical run, the "within-run" random error observed will generally be low (and optimistic) because the results are affected only by those factors that vary in this short time period. This is the best performance possible by the method; if this performance is not acceptable, the method should be rejected or the causes of random error needs to be identified and eliminated before any further testing is carried out.

An experiment conducted over the period of one day, i.e., "within-day", will usually show more variation than a back-to-back within-run experiment unless the method is highly automated and very stable. An experiment conducted over a period of twenty days is expected to provide an even more realistic estimate of the variation that will be seen in patient samples over time. This estimate may be referred to as the "day-to-day", "between-day", or "total" imprecision of the method. NCCLS seems to prefer the term "total imprecision" because it implies that the within-day and between-day components of variability are included [1].

Matrix of sample

The other materials present in a sample constitute its matrix. For example, the matrix of interest for a laboratory test may be whole blood, serum, urine, or spinal fluid. While it may be of interest to measure glucose in each of these types of specimens, it will be difficult to find a single method for all these types of specimens. In evaluating method performance, it is important to use test samples that have a matrix as close as possible to the real specimen type of interest.

Test samples are commonly available as standard solutions, control solutions, patient pools, and individual patient samples. All can be used in a replication experiment, but each has certain advantages as well as limitations.

Standard solutions are often readily available for common chemistry analytes and can be made up to the concentrations of interest. The matrix of standard solutions is usually simpler than that of the real patient samples, e.g., the standard may be aqueous and the patient sample may be serum with a high protein concentration. Thus, an estimate of random error on a standard solution may be optimistic and is likely to represent the best performance available. Still, if that best performance is not satisfactory, a decision can be made to reject the method.

Control solutions or control materials can be obtained from commercial sources in convenient form and size and with long term stability. The matrix may be very similar to that of the patient matrix, but there still may be special effects due to stabilizers, lyophilization and reconstitution, and special additives to enhance the levels of certain tests, such as enzymes and lipids. It may get more difficult in the future to obtain control materials made from actual patient materials because of the need to test and document freedom from infectious diseases. See QC - The Materials for a more extensive discussion of control materials.

Pools of fresh patient samples can often be used for short term testing, particularly within-run and within-day replication studies. Duplicates of fresh patient samples can be analyzed daily over long periods of time, but these samples will still reflect only the within-run and within-day components of imprecision. The between-day component will not be observed unless the duplicates are performed on different days, in which case the stability of the fresh sample must be demonstrated for the time period between the duplicates.

Number of materials and concentrations to be tested

The number of materials to be tested should depend on the concentrations that are critical for the medical use of the test. Generally, two or three materials should be selected to have analyte concentrations that are at medically important decision levels. A medical decision level represents a concentration where the medical interpretation of the test result would be critical.

For cholesterol, medical decision levels are at 200 mg/dl and 240 mg/dl according to the NCEP recommendations for interpreting the result of a cholesterol test [2]. Glucose is typically interpreted at several medical decision levels, such as 50 mg/dL for hypoglycemia, 120 mg/dL for a fasting sample, 160 mg/dL for a glucose tolerance test, and at higher elevations such as 300 mg/dL for monitoring diabetic patients. For guidelines for a wide variety of tests, see the recommendations for Medical Decision Levels provided by Dr. Bernard Statland [3].

Number of test samples

It is commonly accepted that a minimum of 20 samples should be measured in the time period of interest. A larger number of samples will give a better estimate of the random error, but cost and time considerations often dictate that the data are evaluated at the earliest time or minimum period, then additional data collected if necessary.

Data calculations

Random error is described quantitatively by calculating the mean (x), standard deviation (s), and coefficient of variation (CV) from the number, n, of individual measurements, xi, using the following equations:

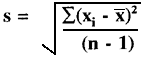
CV = (s/)100

Calculation programs are available on many small calculators, electronic spreadsheets, statistical programs, and specialized method validation software (You can also use the method validation tools on this website!). It is also useful to prepare a histogram of the results to visually display the expected random variation and demonstrate just how large it might get for an individual measurement.

For patient specimens analyzed in duplicate, the standard deviation is calculated from the differences, d, between duplicates, using the following equation:

Criteria for acceptable performance

Although these data calculations are simple, the issue of whether the calculated standard deviation represents acceptable analytical performance is not so simple. The judgment on acceptability depends on what amount of analytical error is allowable without affecting or limiting the use and interpretation of a test result [4,5]. As a starting point for defining the amount of error that is allowable, we recommend using the CLIA criteria for acceptability which have been tabulated on this website.

For short-term imprecision, the within-run standard deviation (s_w-run) or the within-day standard deviation (s_w-day) should be ¼ or less of the defined allowable total error to be acceptable, i.e., s_w-run or s_w-day < 0.25 TE_a .

For long-term imprecision, the total standard deviation (s_tot) should be 1/3 or less of the defined TE, i.e., s_tot < 0.33 TE_a .

Similar judgments on acceptability can be made using a graphical tool - the Method Evaluation Decision Chart [6].

Recommended minimum studies

Select at least 2 different control materials that represent low and high medical decision concentrations for the test of interest. Analyze 20 samples of each material within a run or within a day to obtain an estimate of short-term imprecision. Calculate the mean, standard deviation, and coefficient of variation for each material. Determine whether short-term imprecision is acceptable before proceeding with any further testing.

Analyze 1 sample of each of the 2 materials on 20 different days to estimate long-term imprecision. Calculate the mean, standard deviation, and coefficient of variation for each material. Determine whether long-term imprecision is acceptable.

Future considerations

Somewhat more elaborate experimental designs may be employed to provide more extensive information about the short-term and long-term components of variation. These designs often make use of statistical calculations known as Analysis of Variance (ANOVA), as illustrated in the NCCLS precision performance protocol [1], which will be discussed later in this series of lessons.

References:

1. NCCLS EP5-T2: Precision performance of clinical chemistry devices - Second edition - Tentative Guideline. Wayne, PA:National Committee for Clinical Laboratory Standards, 1992.
2. National Cholesterol Education Program Laboratory Standardization Panel. Current status of blood cholesterol measurement in clinical laboratories in the United States. Clin Chem 1988;34:193-201.
3. Statland BE. Clinical Decision Levels for Laboratory Tests, 2nd ed. Oradell NJ;Medical Economics Books, 1987.
4. Westgard JO, Carey RN, Wold S. Criteria for judging precision and accuracy in method development and evaluation. Clin Chem 1974;20:825-833.
5. Westgard JO, Burnett RW. Precision requirements for cost-effective operation of analytical processes. Clin Chem 1990;36:1629-1632.
6. Westgard JO. A method evaluation decision chart (MEDx Chart) for judging method performance. Clin Lab Science 1995;8:277-283.