Guest Essay

David Plaut, longtime friend and colleague of Dr. Westgard, recently collaborated on a multisite evaluation of the implementation of "Westgard Rules" in the laboratory. The poster, originally at the 2005 AACC conference, is now available in an expanded format online. And we thank David for it.

Dedication: This poster and the work it reflects is dedicated to James Westgard for his efforts through the years to improve the quality of laboratory data and performance while improving efficiency. His on-going efforts to educate the laboratory on many important aspects of quality are without peer. Jim, thank you.

• Introduction
• Methods [briefly]
• Conclusion [briefly]
• Materials and Methods
• Data Analysis
• Results I: Interlab Data
• Results II: CAP survey data
• Results III
• Discussion
• Conclusions

Introduction

In our on-going efforts to improve certain aspects of our laboratory performance including turn-around-time, expenses, and morale, we looked to our QC practices.

Methods

We undertook a study using the CLIA and CAP limits together with the distance our lab mean was from the CLIA or CAP limit (a z-score) as a means to find a better set of QC limits and rules for our chemistry and coagulation departments.

The first step was to evaluate our intralab and interlab data against the CLIA or CAP limit. We used the Dade Behring Dimension® RxL (n = 7) for all our general chemistry tests. For the prothrombin (PT) and activated thromboplastin time (APTT) tests, we used the DadeBehring CA 1500

(n = 6) and 500 (n = 8). In each case, we calculated the distance the lab mean was from the CLIA or CAP limit. This distance is corrected for the bias (lab mean minus the group mean) measured as number of lab SDs.

The Table below illustrates some of the data from the more 500 separate tests/instruments were studied.

In more than 93% of the cases the z-score (lab mean from CLIA/CAP limit) was greater than 3 (in the cases of enzymes, many drug assays and most PT and APTTs the z-scores were >5.0).

These results indicate the three Westgard rules (1 3s, 2 2s and R4s) would be more than adequate for our daily work. We then implemented these rules.

Conclusion

After a period to phase in the new system, we were able to reduce the number of repeats by more than 90%, the turn-around-time, our expenses, the number of calls to the ‘hot line’ and service calls as well as the level of frustration that many felt due to the number of ‘false rejects.’

Materials and Methods

Each of the seven laboratories in this study used the Dade Behring RxL as the main chemistry analyzer. In each case either MAS or BioRad commercial control material was analyzed at least once each 24-hr. period for each level. At the beginning of the study when a control exceeded the 2 SD limits it was repeated (often more than once – until “it came in.”)

After the study and the results compiled and the laboratory staff made aware of why a change was necessary, controls were run only when one of the three rules was broken. (We must admit that there was a period in some laboratories when there was still a ‘tendency’ to hang on to the old way.)

Once the new QC monitoring system was established trouble shooting was done only after one of the three rules failed. Each laboratory has its own protocol for trouble shooting.

For the coagulation part of the study the laboratories used either a Dade Behring CA 500 (n=6) or a CA1500 (n = 6). Two controls were run each 24 hrs and as in the case of the chemistry instruments, repeating the control outside 2 SD (In some cases both controls were repeated.) was the protocol. The same period to phase in the new QC monitoring system was necessary due to some reluctance to give up the old way.

Data Analysis

As illustrated in the tables we used interlab and intralab data to calculate a variety of statistics, including Total Error (TE), % bias, %CV and the z-score. Recall that the z-score or standard score is a way of ‘grading on the (Gaussian) curve. In our case we have set the CAP/CLIA limit as the middle and measured the laboratory mean value from that point in terms to the laboratory’s SD.

Results I: Interlab data

The tables illustrate much of the data collected.

• The relation between % bias and Total Error Allowed (usually a CLIA value).
  
• The precision of the methods.
  
• z-scores that virtually without fail exceed 3.
  
• In the coagulation cases when the data were combined using the worst bias and the worst SD to produce the ‘worst case’ situation, the z-score is still greater than 2.5

These data led us to examine the data from CAP surveys. Representative data from a number of surveys were studied for SDI values exceeding 2 SDI and whether any of those analytes failed that survey.

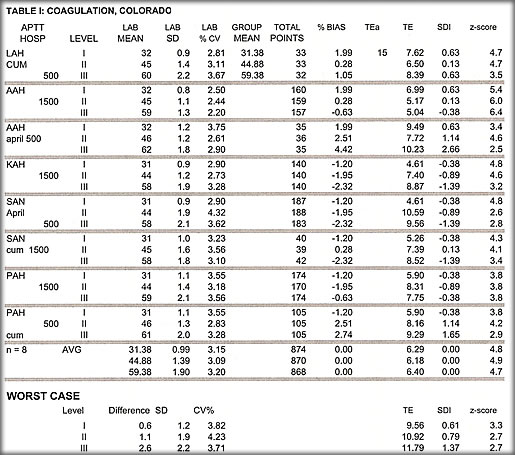
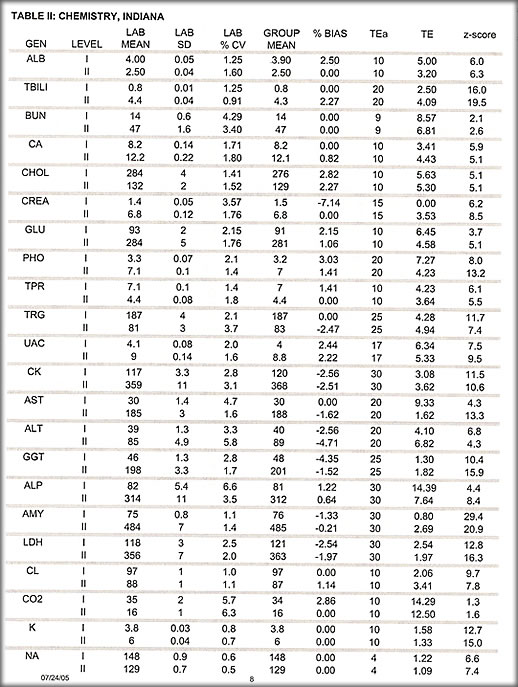
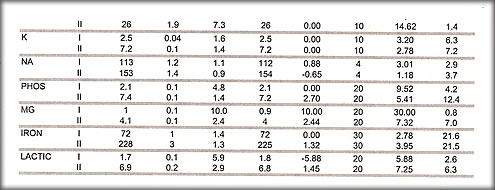
Results II: CAP survey data

1. Colorado Coagulation data

The 219 challenges included 54 PTT; 55 pt; 55 fibrinogen; 55 inr; there were 3 tests that where SDI >2.0 and passed were: 2 fibrinogen and 1 protime. All grades were acceptable.

2. Indiana chemistry

Of 210 challenges on 45 tests there was 1 test where three of 5 challenges exceeded 2 SDI with an average of the 5 of 1.9 SDI passed the survey. None of the challenges had a Z-score of less than 3.75. All grades were acceptable.

3. Indiana coagulation

Of the 20 challenges on 4 tests there were no failures and no tests with an SDI > 2.0. All grades were acceptable.

4. Ohio Chemistry, Instrument I

Of the 30 tests with 120 challenges, there were 6 values where the SDI exceeded 2.0. All grades were acceptable.

5. Ohio Chemistry, Instrument II

Reported on 15 tests with 75 challenges. In one of these 4 of the 5 SDIs exceeded 2.0 with an average for the 5 of 2.1. The lowest z-score was 3.3. All 15 tests received acceptable grades.

In a sentence there were no “unacceptable” results from all labs/all tests/ all challenges while using the suggested flow chart.

Results III

Once the phase-in period was over and the laboratories (generally) accepted the new monitoring system, we noted the following positive outcomes:

There were marked reductions in

1. Repeats and reruns – from the probabilities on the flow chart and our own tabulations reductions in the repeats and reruns were down by at least 85%. This was dependent on the laboratory and the instrument (and the technologist).

2. Co$t$. For a number of reasons, we were not able to quantify this to the degree we wished. However based the fact that repeats were down and turn-around-time was reduced it cannot be argued that our internal costs of reagents, technologist time spent trouble shooting non-problems (WOLF!), and extra maintenance, monies were saved.

3. The staff commented vociferously and emphatically that the change did relieve their level of frustration looking for the (non-existent) problem.

4. Turn around time was reduced in general due to data that once would have awaited rerunning controls were being reported out

10 – 30 min sooner.

Discussion

The results we present here indicate that the original quality monitoring system proposed by Levey and Jennings and revised by Henry using largely manual methods ‘home-brewed’ reagents and calibrators can be replaced, as have instruments and the more variable reagents, with better tools. Modern statistical process monitoring using a system advocated first by Westgard and supported by the AACC and myriad reports and here by our data using a shorter three-rule system unquestionably reduces false rejects without any apparent loss of quality. In additon to the reduction in false rejections, other positive aspects fall out from this system.

Our data more than adequately support a change from the 50-year old approach with 2 SD as a point at which to ‘freak’ toward a more cost-effective, time-saving, easier system beginning with a 3 SD point to freak.

Conclusions

1. From these data for the tests studied as well as various surveys, we have adapted this FLOW CHART based on first three of the “Westgard Rules.”

The probability of a false reject (FR) using these three rules and 2 control points per run is nearly 2* (0.003 + 0.00125 + 0.00125) = 0.015 or 1.5% (down from 10%)!

2. This flow chart reduces the number of repeats by more than 90%.

3. Use of the flow chart reduces turn-around-time due to the reduction in repeats of control.

4. Expenses are reduced even when using a cost per reportable plan.

5. Technologist frustration is reduced therefore morale is increased.

6. Technologist time is saved allowing other productive work to be done.

* Note: If an LIS or HIS is used the 2 SD start is not used; the computer should automatically start with the 1 3S.

** Note: The changes we propose affect only 10% of the data. No changes occur in 90% of what has been happening since QC began!